Why Subscribe?✅ Curated by Tommy Tang, a Director of Bioinformatics with 100K+ followers across LinkedIn, X, and YouTube✅ No fluff—just deep insights and working code examples✅ Trusted by grad students, postdocs, and biotech professionals✅ 100% free
New post from chatomics! Multi-Omics Integration Strategy and Deep Diving into MOFA2
|
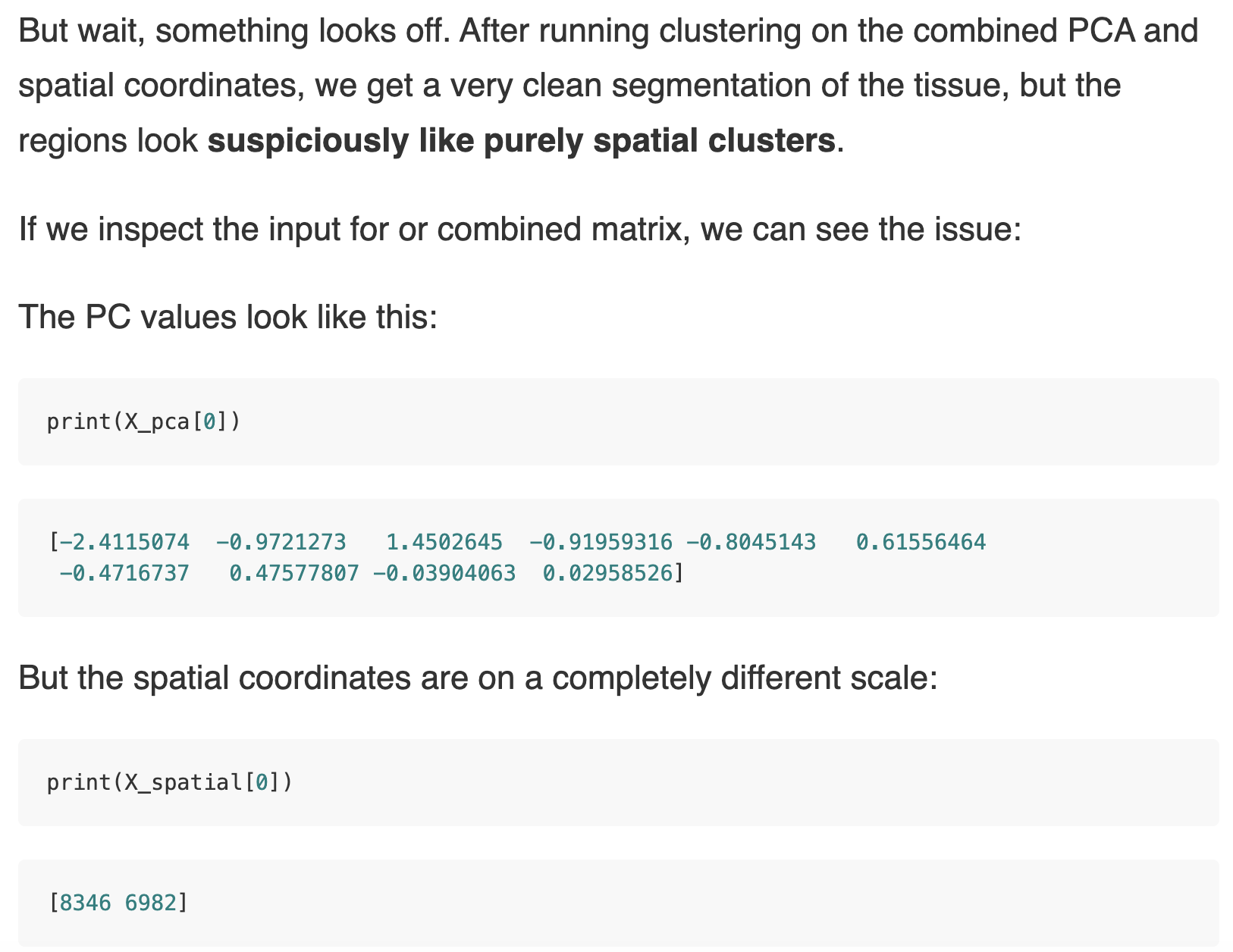
Hello Bioinformatics lovers, I enabled my blog https://divingintogeneticsandgenomics.com/#posts RSS feed. So whenever I have a new blog post, it will be sent to your email. This is different from my weekly Saturday newsletter. My blog posts are mostly technical tutorials. This is new update from my blog: Multi-Omics Integration Strategy and Deep Diving into MOFA2Published on May 17, 2025 Today’s guest blog post on multiOmics integration is written by Aditi Qamra and edited by Tommy.
Multi-omic data collection and analysis is becoming increasingly routine in research and clinical settings. By collecting biological signals across different layers of regulation like gene expression, methylation, mutation, protein abundance etc., the intent is to infer higher order, often non-linear relationships that would be invisible in single-data views. In a previous post on this topic, Tommy walked through the basics of multi-omic integration through an example integrating transcriptomics and mutation data using a linear factor analysis. While this was a great start, multiple methods have been published on this topic from classical multivariate stats to bayesian and graph based models. How to choose the right method for your data and question?The optimal multi-omic integration strategy depends on three things: the biological question, data type, and the objective of our analysis. Start with the biological questionWhat do we want to identify across different data modalities:
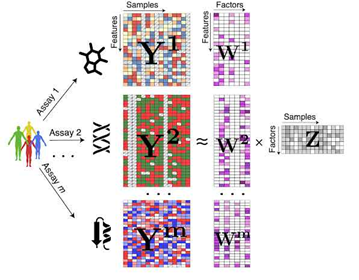
Clarifying this upfront helps determine whether you need an unsupervised factor model, a predictive classifier, or a mechanistic graph-based approach. Interpretability and Biological PlausibilityWhatever the method, results must ultimately be biologically interpretable. This means, we should be able to map back our results to original features (genes, loci, proteins etc.) It is also important to avoid interpreting these statistically inferred patterns since most integration tools are designed to uncover correlations, not causal relationships between omics layers. Orthogonal ValidationFinally, we should always orthogonally validate findings to be able to trust the output of multi-omic methods e.g. Do results align with known biology, be validated through functional assays and/or generalize to other cohorts. Deep diving into one method: Multi Omic Factor Analysis (MOFA2)A frequently asked question when integrating multi-omic data is to identify underlying shared biological programs which are not directly measurable e.g. immune interactions in the tumor microenvironment which may be reflected across different immune and stromal cell proportions, gene expression and cytokine profiles. MOFA2 (Multi-Omics Factor Analysis) is a Bayesian probabilistic statistical framework designed for the unsupervised integration of multi-omic data to identify latent factors capturing sources of variation across multiple omics layers and is well suited to handle sparse and missing data. This was a lot of jargon - Let’s break it down: What is a Probabilistic FrameworkModels like MOFA2 posit that the observed data i.e our collected data modalities is generated from a small number of latent factors, each with their feature-specific weights aka feature loadings, plus noise. But instead of estimating single fixed values for latent factors, feature loadings and noise, it treats them as random variables with probability distributions. Why use Probabilistic ModelingBy modeling the data as probability distributions rather than fixed values, we naturally capture and quantify uncertainty and noise It allows for specification of different distributions per data modality What are Latent FactorsLatent factors are unobserved (hidden) variables that explain patterns of variation in your data. We can infer them from the data by looking for patterns of co-variation across samples and omic layers. NOTE, read Tommy’s LinkedIn post explaining latent space. Models like MOFA2 reduces the dimensionality of the data by identifying these latent factors. Each factor has a continuous distribution per sample as well as weight associated with the all the underlying features of the different data modalities that indicate how strongly they are influenced by each factor.
Notice the factors are shared across all data modalities and weights are specific to each modality - This is what helps capture shared variation and while explaining how latent factors influence the features within each modality. Why Bayesian?MOFA2 is Bayesian because it uses Bayes’ theorem to infer how likely are different values of the latent factors and weights are, given the observed data. It places prior distributions on the unknown parameters and updates these priors using the observed data to infer posterior distributions via Bayes’ theorem. This is where we dive a bit deeper into the maths of MOFA2 (but intuitively): In Bayesian statistics -
Mathematically:
Extending this to MOFA2:
But what about the p(data) ? p(data) is the probability of the observed data under all possible settings of latent factors and loadings, weighted by how likely each setting is under the priors. To compute this, we would have to know every possible combination of latent variables and parameters, which is extremely computationally expensive. But without computing this, we cannot also compute the desired posterior according to the Bayes’ theorem (!) - So what should we do ? Instead of computing the true marginal likelihood (and hence the true posterior) exactly, MOFA2 uses variational inference to approximate it. What is Variational InferenceVariational inference assumes that the true posterior distribution is too complex to work with directly. Instead, it approximates the posterior p(factor, loadings.. | data) by using a simpler family of distributions denoted by q(factor, loadings..), such as Gaussians, even though the true posterior may be much more complicated. It then optimizes the parameters of this simpler assumed distribution (means, variances) to make it overlap as much as possible with the true posterior. At this point, you should stop and ask - “We don’t know the true posterior to begin with, how can we optimize?” The answer lies in the fact that the log of the marginal likelihood, log p(data), is a fixed quantity for a given model and dataset. It can be expressed as: Let’s walk through the new terms:
Tommy’s NOTE: read this blog post by Matt B to understand how variational inference is used in variational autoEncoder. (Warning! mathematical equations heavy, Tommy can not process). What is ELBO
We already know that MOFA2 treats every measurement in each data modality as the model’s predicted value (latent factors × loadings) plus some random noise. It then asks, “How far off is my prediction?” by computing a weighted squared error for each feature—features with more noise count less. Because MOFA2 assumes both its uncertainty and the noise are Gaussian, all those errors collapse into a simple formula that can be computed directly.
MOFA2 starts by assuming every latent factor and every feature loading “wants” to be zero. It treats each as a Gaussian centered at zero ( as we discussed earlier), then penalizes any inferred value that strays too far—more deviation means a bigger penalty. Because these penalties have simple formulas, MOFA2 can compute them exactly to keep most factors and weights small unless the data really demand otherwise.
Since MOFA2’s q(factor, loadings) is just a Gaussian, this “reward for uncertainty” is a simple function of its variances, so it can be calculated directly and helps prevent overfitting. Thus:
By computing each of these in closed form (thanks to Gaussian choices), MOFA2 can efficiently optimize the ELBO and thus approximate the true posterior—all without ever having to tackle the intractable values. Code exampleNow that we have gone through the theory of MOFA2 in a top down approach in deep, lets cover a practical example. We will walk through specific code lines in tutorial accompanying MOFA2 but focus on what each step does rather than trying to replicate it. Using 4 data modalities in CLL_data, the tutorial attempts to identify latent factors capturing variation in mutational, mRNA, methylation and drug response data. It first sets up the model and priors using the When you call The
If you pick the wrong likelihood (e.g. Gaussian on raw counts), the fit will be poor and the ELBO will not converge appropriately. It is thus important to match each modality’s model_opts$likelihoods to your actual data distribution. When you call
Limitations of MOFA2
SummaryBy aligning your biological question, data characteristics, and interpretability requirements you can choose which tool to select for your multi-omic integration analysis. In deeply understanding one such tool
Now that we understand these four pillars, you can pick up and interpret any related multi-omic tool. Happy Learning! Tommy aka. crazyhottommy |
Chatomics! — The Bioinformatics Newsletter
Why Subscribe?✅ Curated by Tommy Tang, a Director of Bioinformatics with 100K+ followers across LinkedIn, X, and YouTube✅ No fluff—just deep insights and working code examples✅ Trusted by grad students, postdocs, and biotech professionals✅ 100% free